![[Dept of Engineering]](../../../engban-s.gif){kind=small}
Hot-Wire Anemometers
Thermal anemometry is the most common method used to measure instantaneous fluid velocity. The technique depends on the convective heat loss to the surrounding fluid from an electrically heated sensing element or probe. If only the fluid velocity varies, then the heat loss can be interpreted as a measure of that variable.
Two fundamentally different sensor types will be discussed below. Cylindrical sensors (hot wires and hot films) are most commonly used to measure the fluid velocity while flush sensors (hot films) are employed to measure the wall shear stress. Hot-wire sensors are, as the name implies, made from short lengths of resistance wire and are circular in section. Hot-film sensors consist of a thin layer of conducting material that has been deposited on a non-conducting substrate. Hot-film sensors may also be cylindrical but may also take other forms, such as those that are flush-mounted.
Thermal anemometry enjoys its popularity because the technique involves the use of very small probes that offer very high spatial resolution and excellent frequency response characteristics. The basic principles of the technique are relatively straightforward and the probes are difficult to damage if reasonable care is taken. Most sensors are operated in the constant temperature mode.
Hot-wire anemometers have been used for many years in the study of laminar, transitional and turbulent boundary layer flows and much of our current understanding of the physics of boundary layer transition has come solely from hot-wire measurements. Thermal anemometers are also ideally suited to the measurement of unsteady flows such as those that arise behind rotating blade rows when the flow is viewed in the stationary frame of reference. By a transformation of co-ordinates, the time-history of the flow behind a rotor can be converted into a pitch-wise variation in the relative frame so that it is possible to determine the structure of the rotor relative exit flow. Until the advent of laser anemometry or rotating frame instrumentation, this was the only available technique for the acquisition of rotating frame data.
Sensors used for the measurement of velocity in turbomachinery investigations are invariably of the cylindrical type. Of these, most are simple hot-wires since these offer the greatest flexibility of use in restricted, often highly unsteady turbomachine environments.
To optimise the frequency response of an anemometer, the probe should have as small a thermal inertia as possible and this is consistent with the requirement of a small size. For work in gases, platinum-coated tungsten of 5 mm diameter is most commonly used (see below) as the sensing element although other sizes and materials are sometimes used. The wire is supported on prongs that are embedded in non-conducting (often ceramic) material.
Typical hot wire sensor
The physics of fluid flow and convective heat transfer are inextricably linked by relationships of the general form
Nu = ƒ ( Re, Pr, Kn, ...geometrical factors )
where the Nusselt, Reynolds, Prandtl and Knudsen Numbers are all non-dimensional quantities. In the context of a cylindrical thermal anemometer, the above equation may be expanded to give
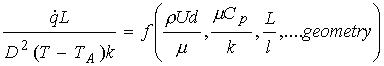
where r is the fluid density, U is its velocity and m its viscosity, d is a typical dimension such as the hot-wire diameter, is the heat loss, L is the wire length, k is the thermal conductivity and l the mean-free path of the fluid and T and Ta the temperatures of the wire and fluid respectively. The geometrical factors referred to include not only the length-diameter ratio of the cylinder L/d but also quantities such as the support geometry for the cylinder and the orientation of the sensor with respect to the flow. It can be seen that the heat loss depends on many parameters.
In 1914, King derived a solution for the heat transfer from an infinite cylinder in an incompressible low Reynolds number flow that may be written as:
Nu = A' + B' Re0.5
where A' and B' are constants so that
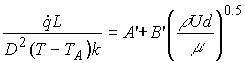
The rate of heat loss to the fluid is equal to the electrical power delivered to the sensor V2/R where V is the voltage drop across the sensor and R is its electrical resistance. If the fluid properties and wire resistance remain constant this expression reduces to
V2 = A'' + B''U0.5
where A" and B" are constants. When the conductive heat losses to the sensor supports or the substrate do not change with fluid velocity, the constant A may be replaced by the quantity V02, where V0 is the voltage across the sensor under zero flow conditions.
In practice, the voltage registered at the anemometer output is not that across the sensor but the e.m.f. E that is applied to the top of the Wheatstone bridge, the two arms of the bridge acting as potential dividers so that the relationship becomes in effect
E2 - A2 = B U0.5
The constant A may be replaced by the zero-flow voltage E0 when high accuracy is not required. In practice, the value of the exponent changes with sensor and velocity as do the values of A and B and its therefore necessary to calibrate each sensor individually and to check this calibration frequently. An exponent of 0.45 is nearer to that found in practice.
Since no universal calibration is available, the sensors must be calibrated. To do this, a low turbulence flow of known velocity must be used. Ideally, the probe should be placed into it in the same attitude that it will be used.
In use, errors arise due to changes in ambient temperature and other fluid properties, and due to the deposition of impurities in the flow on the sensor. Standard procedures are available to correct for the effects of changes in temperature. The time for which a calibration is valid depends on the individual situation. In high speed wind tunnels, large particles can remove a wire with annoying frequency.
If care is taken and calibrations performed at frequent intervals, then an accuracy of better than 1 percent can be achieved for hot-wire velocity measurements in turbomachines.
When a cylindrical sensor is placed so that its axis is not perpendicular to the flow direction, there will be a component of velocity that is parallel to the axis of the sensor. If the sensor has infinite length, then the effective cooling velocity that the sensor experiences is that which is perpendicular to the sensor; the parallel component has no effect. Thus, the effective cooling velocity ueff may be obtained from the expression
u cos a = ueff
where a is the yaw angle between the flow vector and the normal to the axis of the sensor. In the case a wire with a finite length, the temperature is not constant over the length of the wire and aerodynamic perturbations are created by the prongs. These are taken into account by arguing that the component of velocity that is parallel to the axis of the wire now contributes to the cooling effect. A simple probe responds to changes in flow direction in a manner shown in the figure below. The interference of the prongs can be reduced by using prongs that are more widely spaced and plating the ends of the sensing wire with copper or gold to ensure there is little resistance heating except in the central un-plated portion. In this case variation of pitch angle does not effect the response greatly.
It is important to recognise that cylindrical hot-wire and hot-film sensors are capable only of determining the magnitude of the velocity (or a vector component) since the heat transfer is the same whatever the sign of the vector. As a result, conventional sensors are unsuitable for use when the flow reverses such as happens inside separation bubbles. Under these circumstances, specialised multiple sensor probes capable of determining the magnitude and direction of the flow are required.
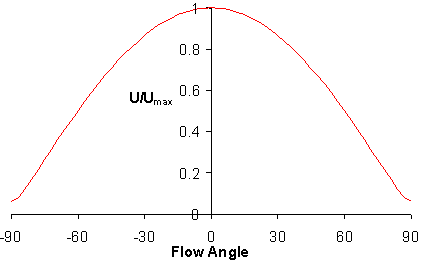
Typical hot wire response curve to yaw angle
Two wires arranged as an X probe can be used to make two-dimensional measurements. In the three-sensor method that is employed when three-dimensional information is required, the three elements of a probe are usually aligned with the axes of a rectangular system of co-ordinates. This probe allows the simultaneous determination of the three velocity components and six turbulence quantities but the spatial resolution is relatively poor. A reduced spatial resolution implies often restricts the effective frequency response much more than the thermal response of the individual sensors.
The calibration and repair of three sensor probes is very time consuming. An alternative technique to using multi-sensor probes involves the use just one sensor but placing the sensor at a number of orientations to the flow. Strictly, only three orientations are required to find the mean components of velocity but the method can be improved by using the method of least squares.
The figure below, shows a typical measurement situation where U is the mean fluid velocity that is normal to the wire and u, v and w are velocity fluctuations in three perpendicular directions. The axis of the sensor is aligned with the w direction so that the sensor will have a very poor response to the w component providing that the length-diameter ratio of the sensor is large (i.e. L/d>200). Therefore, the sensor sees the effective cooling vector U' which, providing v is not too large, has the same magnitude as (U+u') so that at low turbulence intensities the wire is measuring the magnitude of the velocity in the direction of the mean flow. Thus, the stream-wise turbulence intensity 
can be derived by calculating the root-mean-square of the velocity-time history. In isotropic turbulence, this measurement and that of the mean velocity are in error by about 2 percent when the turbulence intensity is about 20 percent.
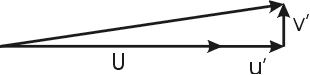
Mean (U) and Instantaneous (u') flow velocities
To obtain the components of turbulence that are normal to the mean flow vector, a variety of two and three sensor techniques are used to determine the magnitude and direction of the instantaneous flow vector. From this, the time-mean and turbulent flow properties may be found.
It is an unfortunate consequence of the laws of heat transfer that when a heated element is positioned close to a solid surface, an increase in heat transfer occurs. A correction must therefore be made to the general form of King's law if accurate measurements of the blade surface boundary layers are to be obtained. In the case of a 5 mm diameter wire, the effect of wall proximity upon the heat transfer extends to 1-2 mm from the surface so that the effects of wall proximity are present in many measurements.
The still-air correction technique is the most commonly used. It involves the measurement of the heat transfer from the wire to the blade surface in still air at the various locations encountered in the experiment. The heat transfer is proportional to the square of the bridge output voltage, E02 in still air. The general form of King's law equation is then modified to give
E2 - A2 - [E02(y) - E02(0)] = B Un
where the constants A, k and n have the same values as determined from a free-stream calibration and the term in the square brackets represents the increased heat transfer.
Home | Current Research | Research Opportunities
Publications | Staff and Students
Research Facilities | Travel Information | Contact Information | Links