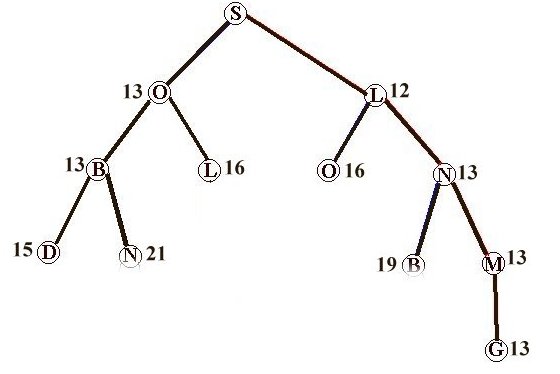
The methods of the previous section found some path between root and goal. A rather harder problem is to find the best path. For this we need to exploit the cost figures in the graph.
This method expands the entire tree using either depth-first or breadth-first search, with the proviso that now search must not terminate when the first root-goal path is found.
This method considers the best path ``so far'' instead of the best successor. It stops only when it has discovered at least one goal and there are no unexplored paths of shorter length than the shortest root-goal path found. (Stopping after the first root-goal path was found would be best-first search.)
Branch and bound efficiency can be greatly improved by using estimates of distances remaining to the goal. Adding this to the actual distance travelled gives an estimate of the total path length. Now one expands the path with the shortest estimate by one generation.
If all estimates were perfect, this would always ensure the optimal path was followed - but of course in practice there will be errors. It is essential to consistently underestimate path lengths. Then the actual distance to some goal can never be shorter than the underestimate of the optimal path, so there can be no premature termination. A heuristic which correctly underestimates the cost/path length to the goal is called an admissible heuristic.
Dynamic programming uses the fact that if the path SI from S to some intermediate point I does not affect the path IG to the goal G, then the minimum path length from SG via I is the sum of the minimum path lengths SI and IG.
How do we choose h(n)?
1) We must underestimate actual cost (E) to avoid premature termination of possible optimal paths to goal.
2) For efficiency must be as close as possible to actual cost.
This method is a straightforward combination of branch+bound, (under-) estimation of remaining distances (i.e. admissible heuristic) and dynamic programming techniques.
The A* algorithm is:
1. Form a queue Q of partial paths. Let the initial Q consist of the zero-cost, zero-step path from the root to nowhere.
2. Until the Q is empty or the goal has been reached, determine if the first path in the Q reaches the goal.2a. If it does, do nothing.3. If the goal is reached, success; else failure.
2b. If is doesn't:2b1. Remove the first path from the Q.
2b2. Form new paths from the removed one by extending one step.
2b3. Add the new paths to the Q.
2b4. Sort the Q by the sum of actual cost so far + the lower-bound estimate of the cost remaining.
2b5. If two or more paths reach (or contain) a common node, delete all but the path which reaches the common node with the lowest cost.
(Implementation of 2b5 may require a separate list of nodes which have been expanded and the lowest costs associated with reaching them.)

Complete: Yes
Time efficient: ?
Space efficient: No
Optimal: Yes