Informed Methods

The next 3 methods use an evaluation function to guide the search towards goal. Information about the state space will be used to guide the search. Knowledge is used in the queueing function to determine which node to expand next. This process uses an evaluation function:

Evaluation function f(n)

Cost: g(n)=C

heuristic: h(n)=E (estimate of distance to goal)

The evaluation function returns a number describing the desirability of expanding the node and uses these numbers to guide the search towards goal.

Method 3: Hill climbing

Search efficiency can be improved if you can estimate whether one choice is likely to be better than another, and order the choices accordingly. This is achieved by obtaining some measure of distance En between a node n and the goal. Sitting at a parent node we would determine the distances Ec1, ... of all its children from the goal. Then expand them in ascending order of E.

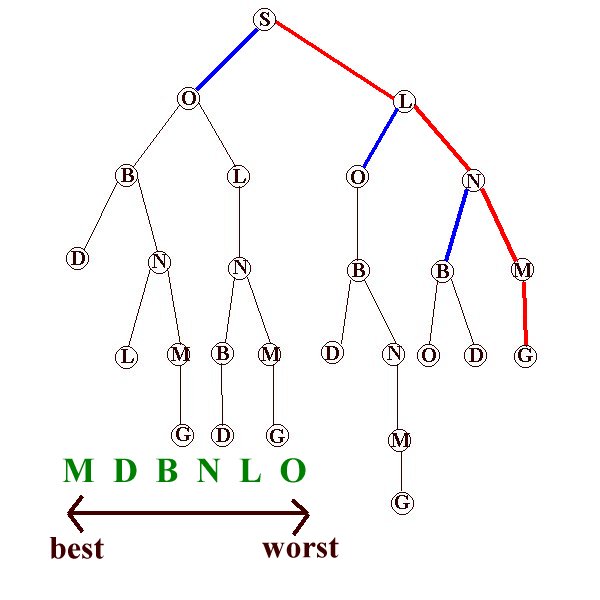
The hillclimbing algorithm is:

1. Form a one element queue Q consisting of the root node.
2. Until the Q is empty or the goal has been reached, determine if the first element in the Q is the goal.
2a. If it is, do nothing.
2b. If is isn't, remove the first element from the Q, sort the first element's children, if any, by estimating remaining distance, and add this sorted list to the FRONT of the Q.
3. If the goal is reached, success; else failure.

We can visualize the disadvantage of this search techniqure by using the hill-climbing analogy.

  1. Local Maxima: If climber starts in foothills, he spends a lot of time climbing to the foothill summits and being disappointed that they are not the goal.

  2. Plateaus If he starts on a flat plain somewhere he will wander aimlessly because local comparison will not determine the best direction.

  3. Ridges If he finds himself on the top a gently sloping most moves will take him down, but he is not at a summit.

Method 4: Beam search

gets round the exponential problem of breadth-first search by expanding only the p most promising nodes at any level, and so at any level k there are only a total of pb nodes. However, this technique is not guaranteed to find a goal.

Method 5: Best-first search

In best-first search expansion of nodes is resumed from the best open node visited so far, no matter where it is in the partially explored tree. The bestfirst algorithm is:

1. Form a one element queue Q consisting of the root node.
2. Until the Q is empty or the goal has been reached, determine if the first element in the Q is the goal.
2a. If it is, do nothing.
2b. If is isn't, remove the first element from the Q, and add the first element's children, if any, to the Q. Sort Q by estimated remaining distance.
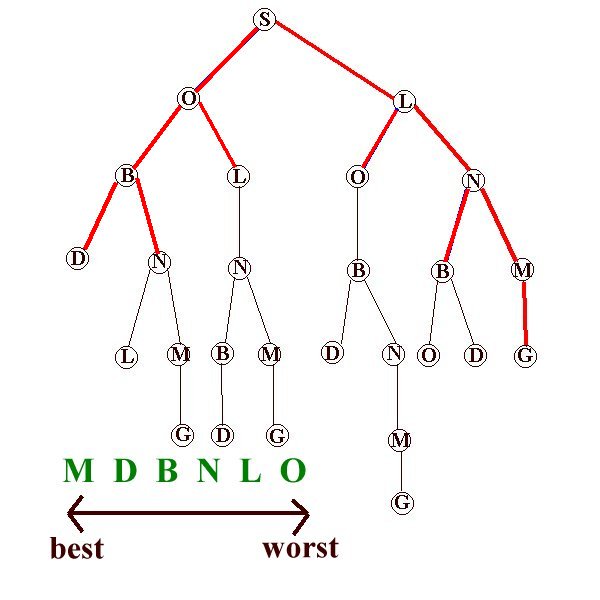
3. If the goal is reached, success; else failure.

Note that Best-first search may NOT find the best path! Finding the optimum path is the subject of the next section.

<<<Previous Next>>>