Propositional Logic
Propositional symbols are used to represent facts. Each symbol can mean what
we want it to be. Each fact can be either true or false.
Propositions are combined with logical connectives to generate
sentences with more complex meaning.
The connectives arre:
 |
AND |
 |
OR |
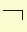 |
NOT |
| => |
implies |
| <=> |
mutual implication |
The meaning (semantics) of the connectives is represented by truth tables.
The following are the truth tables for the connectives:
| Expression | Truth Table | Electrical Equivalent |
|
|
E  F F |
| E¯ F® | True | False |
| True | True | False |
| False | False | False
|
|
 |
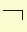 E E |
E
|
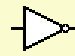 |
E F F |
| E¯ F® | True | False |
| True | True | True |
| False | True | False
|
|
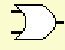 |
| E =>F |
| E¯ F® | True | False |
| True | True | False |
| False | True | True
|
|
- |
|
NOTE(1):
E=> F <=> 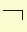 E
=> F .
E
=> F .
NOTE(2): `False True' is a True sentence/assertion.
Implication
A sentence of the form:
E => F
is called an implication with premise (antecedent) E
and conclusion (consequent) F.
Implications are also known as if-then statements or rules.
Its truth table does not quite fit our intuitive understanding
of ``E implies F'' since propositional logic does not require
any relation of causation or relevance between E and F.
It is better to think of ``E F'' as saying:
``if E is true then I am claiming that F is true (otherwise I
am making no claim).
The following commutative, distributive, associative rules apply, as do De
Morgan's theorems.
| Commutative |
E F <=> F F <=> F E
E |
|
E F <=> F F <=> F E
E |
| Distributive |
E (F (F G)<=> (E
G)<=> (E  F) F)  (E (E
 G) G) |
|
E (F (F  G)<=>(E G)<=>(E F)
F) (E (E G)
G) |
| Associative |
E  (F (F  G)
<=> (E G)
<=> (E F) F) G
G |
|
E (F (F  G)
<=> (E G)
<=> (E  F) F) G
G |
| De Morgan's |
C(E F )<=> F )<=>
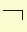 E E
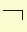 F F |
|
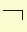 (E (E F )<=>
F )<=> 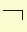 E E
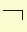 F F |
| Negation |
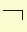 ( ( 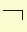 E)
<=> E E)
<=> E |
<<<Previous
Next>>>



E => F .