Autostereoscopic displays produce true three dimensional images of the original, so the perspective of the image must change as one moves closer. How does this happen?

By way of example consider the time-sequentially multiplexed image on a basic 3D display. It is conventional to describe autostereoscopic displays as if there is a finite viewing distance from which the observer's eyes will see the whole of one each of a pair of views, and with a time-sequentially multiplexed basic 3D display this distance is that to where is formed an image of the spot sources of light behind the lens.

However autostereoscopy still works if this distance is made infinite, with the advantage that each view is then an easily computed projection of the 3D image, and that there is no confusion over conventions - the result is sometimes known as "integral imaging". A time-sequentially multiplexed basic 3D display can be configured in this way if the spot sources of light are moved to the focal plane of the lens so that the image of the spot sources of light is formed at infinite distance from the screen of the 3D display. However the viewer is still likely to be only a metre or so from the screen, so what will the viewer see?

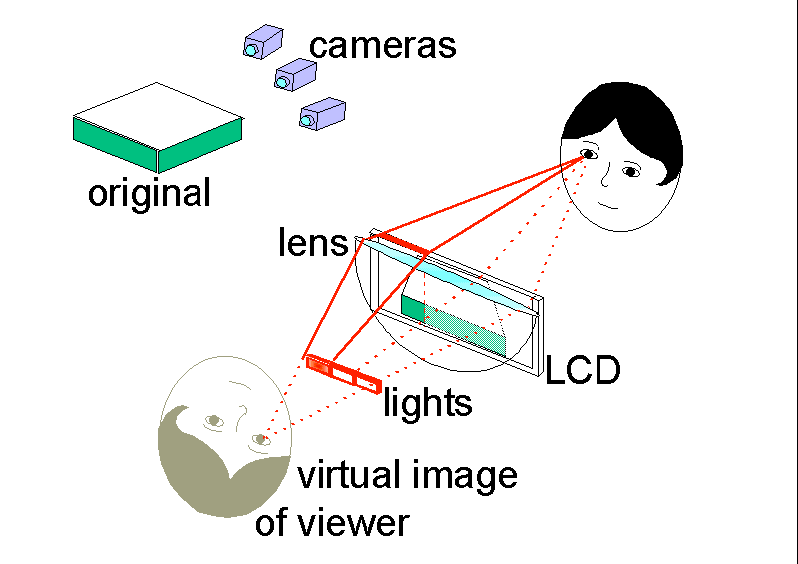
What a viewer sees can be found by using a well-known trick in optics, that of tracing rays backwards, as if they were going from the eye of the viewer to the display instead of vice versa. Do this, continue the rays through the light sources as if they were transparent, and by conventional lens analysis one can construct a virtual image of the viewer's eye some distance behind. Returning to reality, all the rays which are directed into the viewer's eye by the lens of the basic 3D display, must approach the lens as if they came from this virtual image of the viewer's eye.

We can now determine those rays from each illuminator which reach the eye by tracing rays from the virtual image of the viewer's eye through each illuminator in turn as if it was transparent.
 

When the first illuminator is switched on, the first view of the solid object appears on the liquid crystal display. But the image on a liquid crystal display is only visible to an eye if it is illuminated, and the diagram shows that only part of the liquid crystal display is illuminated by rays which travel to the eye. Next, the second illuminator is switched on and the second view of the solid object appears on the liquid crystal display. Once again, only part of this second view is visible to the eye, and the diagram shows that this part is adjacent to the first. In a similar way segments of successive views are made visible to the eye, and since the sequence is repeated faster than the eye can detect, the picture seen by the viewer is a mosaic of segments of different views.

This mosaic of segments is just what the viewer would see if looking at the original three dimensional image. When an eye is close to a cube it is because the angle of the eye relative to one side of a cube is different from that to the other side of a cube that the two lines of the top of the cube appear to converge. Similiarly when an eye is close to a three dimensional image of the cube on an autosterescopic display, it is because the angle of the eye relative to one side of the display is different from the angle relative to the other side that the eye sees segments of different views on either side.